면접을 준비하면서 최근 면접때는 자료구조에 대해서 잘 나오지 않아 생각을 못하고 있었는데, 어제 면접에서 자료구조에 대해서와 장단점 비교에 대한 질문들이 나오게 되었고 나는 당황했다. 그래서 준비가 미비했던걸 인정하고 한번 정리해 보아야겠다. 블로그로 적으면 그래도 한번은 면접때 쭉 볼수 있으니까 말이다.

시간 복잡도에서 대해서 잠깐 알고 아래글을 읽자

아래 글을 읽으면서 시간 복잡도라는 것을 작성했는데, 시간복잡도란 무엇일까?

알고리즘의 로직을 코드로 구현할 때 보통 많이 볼 수 있는데, 시간 복잡도를 고려한다는 말은 ‘입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마만큼 걸리는가?’라는 말이다.

효율적인 알고리즘을 구현한다는 것은 시간복잡도를 고려한다는 말이고 다시 말하면 입력값이 커짐에 따라 증가하는 시간의 비율을 최소화한 알고리즘을 구성했다는 이야기이다.

시간 복잡도는 보통 Big-O 표기법 으로 나타낸다.

Big-O 표기법은 입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마만큼 걸리는가?를 표기하는 방법이다.

자료구조란?

우선 자료구조에 대허서 설명해보려고 한다.

자료구조란 컴퓨터 과학에서 효율적인 접근 및 수정을 가능케 하는 자료의 조직, 관리, 저장을 의미한다.

더 정확히 말해, 자료 구조는 데이터 값의 모임, 또 데이터 간의 관계, 그리고 데이터에 적용할 수 있는 함수나 명령을 의미한다.

어떤 문제에 대해서 효과적으로 적용된 자료구조는 실행시간 혹은 메모리 용량과 같은 자원을 최소한으로 사용하면서 연산을 수행하도록 해준다.

자료구조의 종류

자료구조의 종류는 구현에 따라, 형태에 따라 맞는 방법으로 구현하는 것이 좋은데,

크게는 단순 구조와 자료 간 관계가 1:1인 선형 구조, 1:다 or 다:다 구조인 비선형 구조, 마지막으로 파일 구조로 나누어 진다.

구현에 따라

배열(Array)

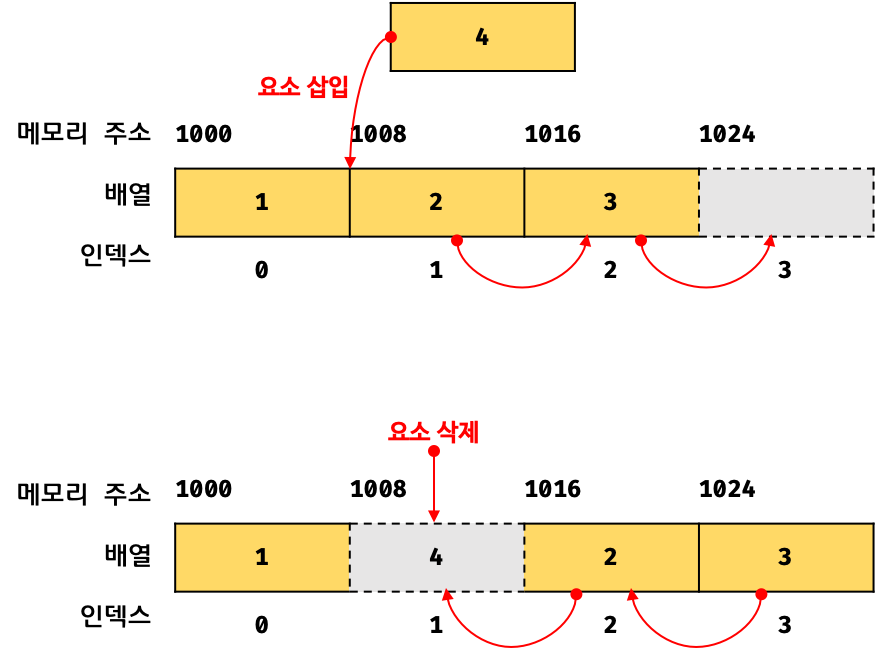
배열 이미지

가장 일반적이고 기본적인 구조이다.
배열은 인덱스(Index)와 인덱스에 해당하는 요소(Element)로 구성된다.
길이가 고정되어 생성된다.(정적 메모리 할당)
인덱스를 통해서 각 요소에 직접 접근할 수 있다.
배열은 논리적 순서와 물리적 순서가 일치한다. 인접한 메모리 위치에 연이어 저장된다.

시간 복잡도

검색(Search) : 요소마다 인덱스를 부여했기 때문에, 특정 요소를 접근하는 시간 복잡도는 O(1)이다. 하지만, 인덱스를 모르는 특정 값을 찾기 위해서는 배열의 모든 요소들을 살펴봐야 하기 때문에 O(n)이다.
추가/삭제(Insert/Delete) : 삽입이나 삭제를 하기 위해서는 길이가 고정되어 있기 때문에 차례대로 한 칸씩 밀어야 하는 과정이 필요하고 그 과정에서 O(n)의 시간 복잡도가 생긴다.

튜플(Tuple) - `자바스크립트에서는 다루지 않음`

둘 이상의 자료형을 묶음으로 다루는 구조이다.
셀수있는 수량의 순서있는 열거 또는 어떤 순서를 따르는 요소들의 모음을 다룬다.
**,**로 구분된 값으로 이루어지는 불변 시퀀스 타입이다.
수정이랑 삭제가 되지않아 읽을 수만 있게 하고 싶을때 또는 수정하면 안 되는 자료를 쓸때 사용한다.

연결 리스트(LinkedList)

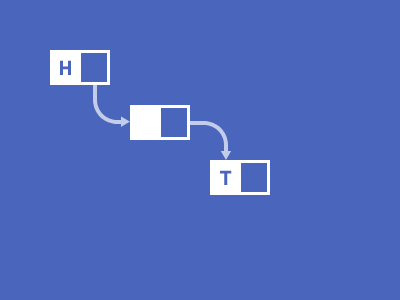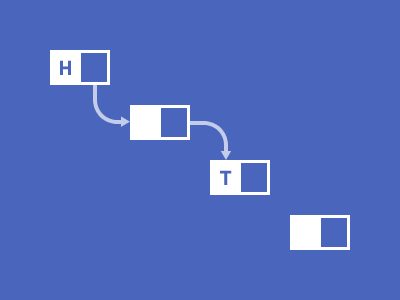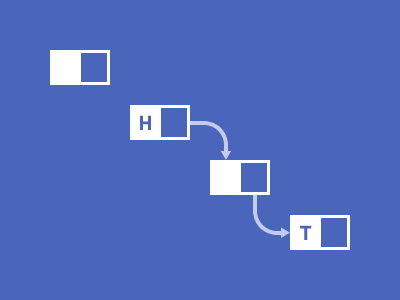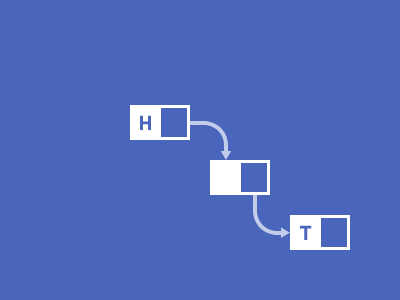
연결 리스트 이미지

배열의 추가/삭제 연산에 대한 비효율성을 극복하고자 등장한 데이터 구조이다.
- 요소를 접근할때 순차적으로 접근해야되는 특성을 가진 배열과 동일하게 링크드 리스트도 순차적 접근을 해야 한다.
- 배열과 다르게 인덱스를 가지고 물리적 배치를 사용하지 않고, 참조 시스템을 사용한다.
노드를 단위로 구성되어 있으며, 노드는 초기값 또는 입력된 값과 다음 노드를 가리키는 참조값으로 구성되어 있고 노드가 다음 요소에 대해 가르키지 않고 있다면 리스트의 끝이라 판단한다.
새로운 요소가 추가될 때 런타임에 메모리를 할당한다.(동적 메모리 할당)
연결 리스트는 아래와 같이 목적 방식에 따라 구현할 수 있다.
- 원형 연결 리스트 : 각 노드는 다음 노드를 가리키고, 마지막 노드가 처음 노드를 가리키는 연결 리스트이다.
- 이중 연결 리스트 : 각 노드는 이전 노드와 다음 노드를 가리키는 참조값으로 구성된다. 처음 노드의 이전 노드와 마지막 노드의 다음 노드는 없다.
- 환형 이중 연결 리스트 : 처음 노드가 이전 노드로 마지막 노드를 가리키고, 마지막 노드가 다음 노드로 처음 노드를 가리키는 이중 연결 리스트이다.

시간 복잡도

검색(Search) : 처음부터 순차적으로 접근해야 하기 때문에 O(n)의 시간 복잡도를 갖는다.
추가/삭제(Insert/Delete) : 동적인 메모리 크기를 갖기 때문에, 새로운 요소를 추가하거나 삭제할 경우에 해당되는 부분만 변경하면 되기 때문에 O(1)의 시간 복잡도를 갖는다.

해시 테이블 (Hash Tables / Hash Map)

Hash Tables 이미지

개체가 해시값에 따라 인덱싱된다.
대량의 정보를 저장하고 특정 요소를 효율적으로 검색할 수 있는 복잡한 데이터 구조다.
해시 테이블을 구현하기 위해서는 연결 리스트(LinkedList)와 해시 함수(Hash FUnction)이 필요하다.
특정한 키(key)에 대해서 해시 함수 또는 해시 알고리즘을 통해 일정한 길이의 해시(hash)를 만들어내고, 버킷(bucket)에 저장한다. 이후에 같은 키에 대해서 같은 해시를 만들어내고, 해시를 통해 해당 값(value)을 조회할 수 있다.
해싱(Hashing)은 해시 함수를 통해서 임의의 값을 고정된 크기의 값으로 변환하는 작업을 말하는데, 키 값을 입력받아서 해시 함수를 통해 얻은 해시(Hash)를 배열의 인덱스로 환산해서 값에 접근하는 것을 의미한다.
하지만 입력된 키의 해시 값이 이미 데이터가 저장된 버킷을 가리키어 해시 충돌이 일어날 수 있는데, 해시 충돌은 자료구조나 알고리즘의 효율성을 떨어지기 때문에 해시 함수는 해시 충돌이 자주 발생하지 않도록 구성되어야 한다.

충돌 해결 방법

분리 연결볍(Separate Chaining) : Linked List 혹은 Tree를 사용하는 방법이다. 충돌이 발생하는 경우 인덱스가 가리키고 있는 값에 노드를 추가하여 값을 추가한다. 대신, 두 방법 모두 많이 추가하면 비효율적이다.
개방 주소법(Open Addressing) : 해시 테이블의 빈공간을 사용하는 방법이다. 추가적인 메모리 공간을 필요하지 않은 장점이 있다. 그 방법에는 Linear Probing, Quadratic Probing, Double Hashing 등이 있다.

시간 복잡도

키 값을 배열의 인덱스로 사용하기 때문에, 값을 직접 접근할 수 있다. 따라서, 해시 테이블의 평균 시간 복잡도는 O(1)이다.(충돌(Collision)이 일어나는 경우 O(n))

형태에 따라

선형 구조

스택(Stack)

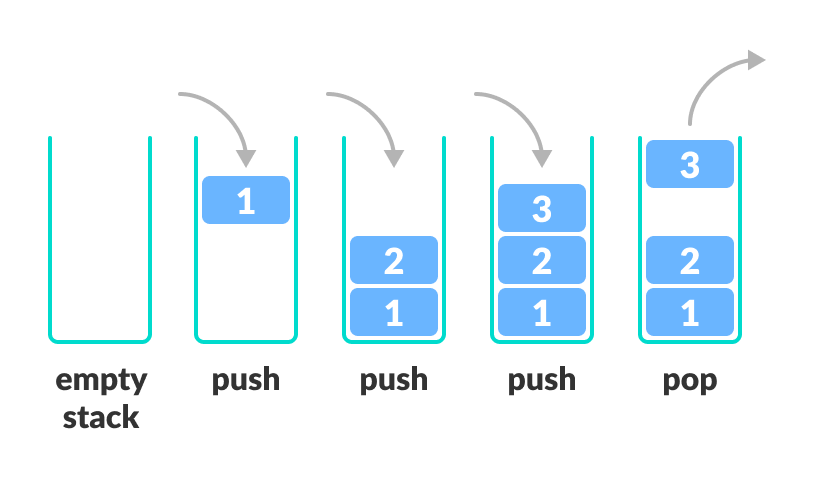
Stack 이미지

스택 자료구조는 후입선출 방식으로 먼저 저장된 것이 꺼내어 슬 때는 제일 나중에 나온다.(LIFO(Last In First Out) 메커니즘) 반대로, 가장 최근에 저장된 것이 꺼내어 쓸 때는 제일 먼저 나온다. 만약, 자료들의 나열 순서를 바꾸고 싶다면 스택에 집어 넣었다가 꺼내면 역순으로 바뀐다.
동적 메모리 방식을 취한다.

시간 복잡도

검색(Search) : 처음부터 순차적으로 접근해야 하기 때문에 O(n)의 시간 복잡도를 갖는다.
추가/삭제(Insert/Delete) : 가장 위에 데이터를 추가하거나 삭제하기 때문에 O(1)의 시간 복잡도를 갖는다.

큐(Queue)

Queue 이미지

스택과 반대로 큐 자료구조는 선입선출 방식으로 먼저 저장된 것이 제일 먼저 나온다.(FIFO(First In First Out) 메커니즘) 반대로, 가장 나중에 저장된 것이 꺼내어 쓸 때는 가장 나중에 나온다.
동적 메모리 방식을 취한다.
환형 큐 : 한정된 길이 안에서 부수적인 작업 없이 읽고 쓰기를 할 수 있는 큐이다.

시간 복잡도

검색(Search) : 처음부터 순차적으로 접근해야 하기 때문에 O(n)의 시간 복잡도를 갖는다.
추가/삭제(Insert/Delete) : 추가는 front에서만 일어나고 삭제는 항상 rear에서만 일어나므로 O(1)의 시간 복잡도를 갖는다.

덱(Deque)

Double-ended queue의 약자로 삽입과 삭제가 양쪽 끝에서 모두 발생할 수 있는 선형 자료구조이다.
덱이라고도 불리지만 양방향 큐라고도 불리는 듯하다.

비선형 구조

그래프(Graph)

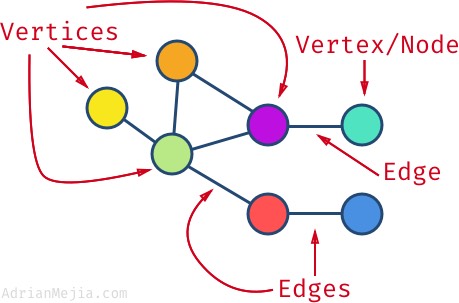
Graph 이미지

객체 간의 연결(Edge)을 시각화한 것으로 정점(Vertex)간의 관계를 표현하는 자료구조로 꼭짓점과 꼭짓점을 잇는 단순한 형태의 자료구이다.
그래프는 변이 방향성을 가지는 가, 안가지는 가에 따라서 그래프를 분류할 수 있는데, 방향성이 있다면(Directed) 없다면(Undirected)
새로운 요소들의 추가/삭제가 용이하고 효율적이다.
그래프 역시 입력된 키의 해시값이 이미 데이터가 저장된 버킷을 가르킬 수 있기 때문에 충돌이 일어날 수 있다.
유향 그래프(Directed) : 변의 방향은 보통 부모를 가리키도록 구현된다.
무향 그래프(Undirected) : 순환이 없는 연결 그래프로 구현된다.

시간 복잡도

그래프(Graph)의 시간 복잡도∙공간 복잡도는 노드(N), 정점(V), 엣지(E)를 사용하여 표현한다.

두 노드의 연결 확인 : 인접 행렬의 경우 고유 인덱스로 바로 접근 가능하여 O(1)의 시간 복잡도를 갖는다. 인접 리스트의 경우 한 노드의 인접 리스트 안의 특정 노드가 있는지 확인해야 하기 때문에, 최악의 경우 전체를 봐야하므로 O(N) or O(V)의 시간 복잡도를 갖는다.
한 노드에 연결된 모든 노드 확인 : 인접 행렬의 경우 특정 노드를 나타내는 행렬을 돌아서 연결된 노드를 가져와야 하기 때문에, O(N) or O(V)의 시간 복잡도를 갖는다. 인접 리스트의 경우 연결된 노드의 갯수는 곧 엣지의 갯수이므로, 엣지의 갯수만 확인하면 되므로 O(E)의 시간 복잡도를 갖는다.
추가/삭제(Insert/Delete) : 추가의 경우 노드/정점이나 엣지 모두 O(1)의 시간 복잡도를 갖는다. 하지만, 삭제의 경우에는 노드/정점의 경우 특정 노드/정점을 찾는 시간과 그와 연결된 엣지를 삭제해야 하므로 O(N+E) or O(V+E)의 시간 복잡도를 갖는다. 엣지의 경우 특정 엣지를 찾는 시간이 소요되므로 O(E)의 시간 복잡도를 갖는다.

트리(Tree)

Tree 이미지

노드로 구성된 계층적 자료구조이다.
뿌리와, 뿌리 또는 다른 꼭짓점을 단 하나의 부모로 갖는 꼭짓점들로 이루어진 구조이며, 부모 자식 관계는 변으로 표현된다.
최상위(Root)노드를 만들고, 부모(Parent)노드에 자식(Child)노드를 추가하고 그리고 그 자식 노드가 부모 노드로써 또 다른 자식 노드를 추가하는 구조를 가지고 있다.
트리에 또 다른 트리가 있는 재귀적 자료구조이다.
트리는 아래와 같이 목적 방식에 따라 구현할 수 있다.
- 이진 트리(Binary Tree) : 모든 노드들이 둘 이하의 자식을 가진 트리
- 이진탐색 트리(Binary Search Tree) : 이진탐색(binary search)과 연결리스트(linked list)를 결합한 방식
- 균형 트리(Balanced Tree) : 이진 탐색트리에 새로운 노드가 삽입이 되면 부모의 노드보다 작은 값은 왼쪽으로 큰 값은 오른쪽으로 추가하면서 서브트리가 계속 구성되는 방식
- 힙 트리(Heap Tree) : 부모의 값은 항상 자식(들)의 값보다 크거나(Max heap), 작아야(Min heap)하는 규칙을 가진 트리로 여러개의 값 중에서 가장 크거나 작은 값을 빠르게 찾기 위해 만들어짐

시간 복잡도

일반적인 Tree의 시간복잡도는 아래와 같다.

검색(Search) : 특정 값을 탐색하거나, 조회 할 때 O(n)의 시간복잡도
추가(Insert) : 특정 노드의 child node를 생성해주려면 특정 노드를 찾고 O(n), 그 노드의 childNode에 추가하면 O(1)의 시간복잡도를 가진다.
삭제(Delete) : 삭제하고자 하는 노드의 부모 노드를 찾은 뒤에 O(n) 삭제하고자 하는 노드를 부모 노드의 childNode 리스트에서 지워주면 O(1)의 시간복잡도를 가진다.